三、我们将说明内生选择偏倚为什么在因果推断中很重要。在因果推断中，所有的非参数识别问题都可以归入下列三种问题：过度控制偏倚（overcontrol bias）、混杂效应偏倚、内生选择偏倚。内生选择抓住了名字各异的偏倚的共同结构，包括选择性不回应（selective nonresponse）、确认偏倚（ascertainment bias）、损耗偏倚（attrition bias）、基于已知信息的截取（informative censoring）、Heckman选择偏倚（Heckman selection bias）、样本选择偏倚（sample selection bias）、同质相吸偏倚（Homophily bias）等。

四、我们将解释没将因变量纳入分析时为什么内生选择偏倚还会发生。内生选择偏倚可以来自于很多地方。它可以来自于对结果变量的条件化，也可以来自于对受结果变量影响的变量的条件化还可以来自于，时间上先于结果变量的变量，甚至可以来自于时间上先于处理的变量（Greenland 2003）。

五、可能是最重要的一点，我们将通过例子说明，内生选择偏倚在分层研究，文化社会学、社会网络分析、政治社会学、社会人口学，以及教育社会学中都普遍存在。

本文所提及的方法论上的要点，都曾在计量经济学、统计学、生物统计学、计算机科学的文献中多次出现。我们的创新之处在于，我们用图作为表示方式，将这些要点联合起来，呈现给社会学家。具体来说，我们使用了有向无环图（directed acyclic graph，简称DAG；Pearl 1995, 2009; Elwert 2013）。它是传统的线性的路径图（path diagram；Wright 1934, Blalock 1964, Duncan 1966, Bollen 1989）的非参数推广。有向无环图严谨、形式，却仍然十分易懂。它依赖图的运算规则，而非代数的运算规则。我们希望这种呈现方式能够让没有接受多少数学训练的社会学家明白，什么时候以及为什么，内生选择偏倚可能会让经验研究产生问题。

我们从技术的说明开始。第二节描述非参数识别的概念。第三节介绍有向无环图。第四节解释，两变量间的因果、混杂、内生选择三者间在结构上有何关联，并说明可以怎样用有向无环图来把因果关系和伪关联（spurious association）分开。第五节是本文的核心，我们将介绍大量应用上牵涉到内生选择偏倚的例子。第六节做总结，反思如何在实践中处理内生选择偏移的问题。

2. 识别vs. 估计

在这里，我们把内生选择偏倚看做是怎样识别因果效应的问题。跟从现代因果推断文献的做法，我们将因果效应定义为潜在结果（potential outcomes）间的差异（Rubin 1974, Morgan & Winship 2007）。因为因果效应不可能被直接观察到（Holland 1986），所以我们很难从数据中还原因果效应。因果效应只能从观察到的关联性中推断出来。但通常我们想要知道的因果效应和各种非因果伪性成分一同混在观察到的关联中。因果识别的任务就是将关联中因果的成分跟伪性成分干净地分开。如果能够找到了一种方法，能够在样本量无限且没有测量误差时有去除关联性中所有非因果成分的可能性，使得关联性中只剩下我们感兴趣的因果效应，那么我们就说这个因果效应被识别了。

识别分析（identification analysis）需要对数据的生成模型做出假设。就好比说，识别教育对工资的因果效应。如果一个人认为能力对教育和工资都有正面效应，那么教育与工资间的边缘（也就是未调整的）关联性（marginal association）没有使教育对工资的因果效应被识别。但如果一个人假设能力是唯一同时影响教育和工资的因素，那么在完美地对能力做调整后，教育跟工资间的条件关联性（conditional association）就能使教育对工资的因果效应被识别。遗憾的是，分析者没有办法用经验研究来完全证明数据生成模型的假设（Robins & Wasserman 1999）。所以，分析者需要明确说明自己对数据生成模型的假设，让其他学者来检查、评判。我们用有向无环图来清楚地说明数据生成模型。

非参数识别指的是只需要对数据生成过程做出质性因果假设，无需对变量的分布（如联合正态性）或是因果关系的函数形式（如线性）做出参数假设就能做出的识别。我们认为本文的关注点是种强项，因为社会学家每天都会做因果性的陈述，相比之下，分布形式或是函数形式的假设经常缺少社会学上的辩护。

（假设理想数据的）识别是（使用真实数据的）无偏误估计的必要先决条件。现在我们还没有在各种有内生选择偏倚的情况下都能够估计因果效应的通用办法（Stolzenberg & Relles 1997, p. 495）。所以我们这里着重说明识别的问题，只在段落衔接处处理估计的问题。Pagan & Ullah （1997）、Vella （1998）、 Grasdal (2001）、Christofides et al. （2003） 综述了计量经济学文献中对怎样在有内生选择时估计因果效应的讨论。这些文献包含对Hausman & Wise （1997）的截尾回归模型（truncated regression model）和Heckman （1976, 1979）的经典两步估计方法（two-step estimators）。Bareinboim & Pearl （2012）在图取向框架下讨论了有内生选择时的估计问题。流行病学和生物统计中，基于Robins框架（1986, 1994, 1999）的文献逐年增多，讨论了处理随时间变化时内生选择的问题。

3. 有向无环图简介

有向无环图可以编码分析者对总体数据生成过程的质性因果假设。这些假设集合在一起，构成了分析者做识别分析的模型基础、理论基础。有向无环图由三个元素组成（图1）。第一，字母表示随机变量。随机变量可能被观察到了，也可能没有被观察到。变量可以有任意分布，可以是连续的或者是离散的。第二，箭头表示直接的因果效应。直接的效应可以有任意的函数形式（线性或非线性），也可能在不同个体间有程度上的差异（效应异质性），以及在某些约束下（Elwert 2013），他们可能会随着其他变量的值的改变而改变（交互效应或调节效应）。因为未来事件不能导致过去事件发生，箭头给定了两变量时间上的先后顺序，以使有向无环图中不包含有向的环。第三，箭头的缺失就表示变量间没有因果效应。用经济学的说法来说，箭头的缺失表示排除性限制（exclusion restriction）。举例，图1排除了箭头U→T和X→Y。缺失的箭头是推断因果信息必需的。

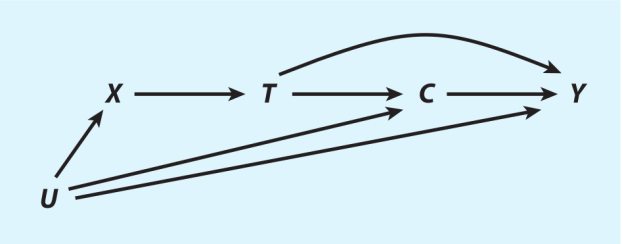
图1

为了清晰起见，我们假设本文中的有向无环图画出了其描述的数据生成过程中所有观察到和没有观察到的共同前因变量。注意，这个假设的必要条件是变量的所有其他输入都边缘独立，也就是所有变量都有独立的误差项。这些独立的误差项不需要在有向无环图中画出来，因为他们对非参数识别没有帮助（当偶尔他们会妨碍识别时，我们会将他们画出来）。

路径（path）指的是连接两个变量的一系列箭头，不管箭头的方向如何。一条路径至多能够经过某个给定变量一次。因果路径是在处理与结果间的路径，其中所有的箭头都背对处理，指向结果。判断因果路径是否存在、大小如何，分别是因果检验和因果估计的任务。所有因果路径组合在一起就是总因果效应（total causal effect）。除非另有声明，本文关心的是平均总因果效应（average total causal effect）的识别。图1中，T对Y的总因果效应包含因果路径T→Y和T→C→Y。所有其他处理与结果间的路径都叫做非因果路径（或伪路径），例如T→C←U→Y和T←X←U→Y。

本文讲条件化时只指条件化于某个变量。更宽泛地说，条件化指的是将关于某个变量的信息通过某种手段引入到分析中。在社会学中，条件化的通常形式包括在回归模型中控制某个变量，做特定组别分析（因而条件化于某个组别），或是选择性地收集数据（如在调查中排除儿童，囚犯，退休人员，以及无回应者）。本文用在被条件化的变量上面画个框来表示条件化。

4. 关联的来源：因果、混杂和内生选择

4.1 基石：因果、混杂和内生选择

有向无环图很厉害。它能够展示出一个质性因果模型所有的边缘独立、条件独立、边缘关联、条件关联（Pearl 2009）。这让分析者有办法分辨出哪些关联是纯粹因果性的，哪些关联不是——也就是让分析者有了种非参数识别分析的正式办法。在没有抽样变异（也就是偶然性）时，所有可观察到的关联都仅仅来自于三类基础配置：链（A→B，A→C→B，等），叉（A←C→B），以及反转叉（A→C←B）（Pearl 1988, 2009; Verma & Pearl 1988）。这三种配置对应关联的三种来源，因果，混杂偏倚，以及内生选择偏倚。

图2

首先，如果一个变量直接或者间接地导致了另一个变量，那么两个变量间有关联。在根据这个有向无环图生成的数据中，A与B之间观察到的边缘关联会反映出纯粹的因果关系——也就是说，A与B之间的边缘关联识别出了A对B的因果效应。对比之下，对图2b的中间变量C条件化就会挡住这条因果路径，因此A对C的因果效应被控制掉了。所以，给定C时，A与B之间的条件关联是零，无法识别A对B的非零因果效应。我们说，对从处理到结果的因果路径上的变量做条件化会引发过度控制偏倚。

其次，如果两个变量有共同的前因，那么两个变量间有关联。在图3a中，A和B有关联，因为他们都是由C导致的。这就是我们熟悉的混杂偏倚——A与B之间的边缘关联不是对A对B因果效应的识别。对图3b中的C做条件化，能够使得这种伪关联消失。因此，A与B之间给定C的条件关联识别了A对B的因果效应。该因果效应在此图中为零。

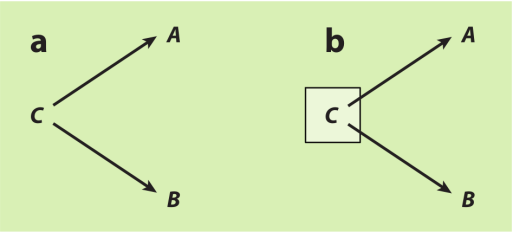
图3

第三种两变量间可能有关联的原因比较少人知道，但正是本文的中心点：条件化两变量的共同结果（也就是碰撞变量，collider），会导致两变量间产生虚假的关联。我们把它叫做内生选择偏倚。在图4a中，A与B边缘独立，因为他们间既不是一个导致了另一个的关系，也没有共同的前因。因此，A与B之间的边缘关联识别了他们间的因果效应（在此图中为零）。在图4b中，相反，条件化于碰撞变量C导致了没有连接的两个前因A与B产生了关联。因此，A与B间给定C的条件关联，被用于估计A与B之间的因果效应时，是有偏误的。两个没有连接的变量间的虚线表示了他们间的伪关联。这种虚线的效果跟平常路径中的一条线段无异。对碰撞变量导致的变量（碰撞变量的派生变量，descendants）条件化跟条件化碰撞变量本身有同类的效果（图4c），因为这个派生变量是碰撞变量的代理测度。

图4

内生选择不明显，很难从抽象上明白，我们先给出个直观的人造例子来解释图4的内容。考虑才能（A），美貌（B），在好莱坞成功（C）三者间的关系。为了说明，我们假设在一般人群中美貌与才能无关（也就是，美貌不导致才能，才能不导致美貌，而且他们间也没有共同的前因）。进一步假设，只要有了美貌与才能任意一者，演员就能在好莱坞里成功。在这些假设下，成功明显是个碰撞变量。现在我们条件化碰撞变量。比如说，条件化的方式是只在成功的好莱坞演员里看美貌与才能间有无关联。在我们对成功的模型之下，一个演员没有才能，但却是一个成功的演员，那么他一定很美。反之，一个人，不能说他美，但却是个成功的演员，那么他一定有才能。不管是哪种方式，对碰撞变量（成功）条件化，造出了在成功者中美貌与才能间的伪关联。这种伪关联就是内生选择偏倚。

这个例子可能缺少社会学意义，但它说明了内生选择偏倚的逻辑——条件化于共同的结果会扭曲这个结果的前因间的关联。如果想让例子变得更加贴近现实，我们可以放松假设，比如说允许A导致B（可能有才能的演员不那么注重让自己变美）。然而，内生选择的问题不会消失。才能与美貌间所观察到的条件关联仍有偏误，不能当作才能对美貌的真实因果效应。在给定变量集里增加箭头对非参数识别不会有帮助（Pearl 2009）。不幸的是，我们在没有额外的假设时不能预测内生选择偏倚的符号与大小（Hausman & Wise 1981, Berk 1983, VanderWeele & Robins 2009b）。

总结，过度控制偏倚、混杂偏倚、内生选择偏倚是完全不同的现象。他们从不同的因果结构中诞生，需要的补救方法也不同。图2，3，4间的区别清晰地总结了这种不同。过度控制偏倚来自对处理与结果的因果路径中的变量的条件化，其补救方法是不要条件化因果路径中的变量。混杂偏倚来自于没有成功条件化处理与结果的共同前因，其补救方法是条件化共同的前因。最后，内生选择偏倚来自于条件化连接处理与结果间非因果路径上的碰撞变量或其派生变量。其补救方法是不要条件化这样的碰撞变量及其派生变量。三种偏倚全部都源自分析错误，尽管错误不同：混杂源自分析者没有条件化应该条件化的变量；过度控制和内生选择则源自分析者条件化了不应该条件化的变量。

4.2一般有向无环图中的识别

所有有向无环图都是由链、叉、反转叉建成的。因此，了解了链（因果）、叉（混杂）和反转叉（内生选择）对关联性有何含义，就能够对任意复杂的因果模型做非参数识别分析。所谓的d分离规则总结了这些内在意义（Pearl 1988, 1995; Verma & Pearl 1988）：

首先，要留意到，在有向无环图上，所有的关联性都由路径传递，但不是所有路径都传递关联。对于两个变量A与B间的路径，若：

1. 路径中包含已被条件化的非碰撞变量C，A→[C]→B，或A←[C]→B；或

2. 路径中包含碰撞变量C，且碰撞变量或是其派生变量都没有被条件化，A→C←B，

则该路径没有传递关联性。我们说这条路径被阻断了，被关闭了，或是被d分离了。

没有被d分离的路径被称作是开放的、没有被阻断的、d连结的，他们传递关联性。在所有路径中都被d分离的两个变量在统计上独立。反之，在至少一条路径中d连结的两个变量在统计上有关联（Verma & Pearl 1988）。

重要的是，条件化碰撞变量和条件化非碰撞变量会产生相反的效果。条件化非碰撞变量阻断关联性在路径上的流动，而条件化碰撞变量打开路径上关联性的流动。

依此，我们可以通过判断我们能否用条件化某些变量的方法，使所有处理与结果间的非因果路径被阻断，同时使处理与结果间的因果路径保持开放，来确定一个因果效应是否可以被识别。例如，在图1中，T对Y的总因果效应可以通过对X条件化识别，因为X不再从T到Y的因果路径中，且对X条件化阻断了T与Y之间的两条非因果路径，T←[X]←U→Y和T←[X]←U→C→Y（T与Y之间的第三条非因果路径，T→C←U→Y，被无条件地阻断了，因为它包含碰撞变量C。条件化C会破坏识别，有两个原因：一是这会引入内生选择偏倚，因为非因果路径T→[C]←U→Y被打开了；二是这会引入过度控制偏倚，因为C在T到Y的因果路径上，T→[C]→Y）。

我们之所以想要写这篇文章，就是因为打开非因果路径实在是太简单了，一不留神就会引入内生选择偏倚。我们下面讨论社会学有什么这类偏倚的例子。

5. 社会学中内生选择的例子

条件化因果过程中任何地方的碰撞变量都可能产生内生选择偏倚。它可以产生于对结果后的碰撞变量的条件化，可以产生于对处理和结果间的碰撞变量的条件化，可以产生于对在结果前的碰撞变量的条件化（Greenland 2003）。因此，我们根据碰撞变量相对处理和结果的时间点来组织下面的例子。

5.1条件化结果变量（后）的碰撞变量

众所周知，直接对结果进行选择，还有条件化被结果影响的变量，会导致偏倚。不管如何，这两种问题仍继续在社会学的经验研究中发生。问题可能因搜集数据时非随机的抽样计划产生，或是从数据分析时看起来很有说服力的选择中产生。我们在此给出些经典例子，还有近来的例子。我们将说明他们怎样通过对碰撞变量的条件化引入了内生选择偏倚。

样本截断偏倚（sample truncation bias）。Hausman & Wise（1977）对样本截取偏倚的有力分析为我们提供了一个内生选择偏倚的经典例子。他们考虑的问题是怎样在仅选择（截取）了低收入者的样本中估计教育对收入的影响。图5描述了问题的核心。收入I被教育E影响，同时也被其他因素影响。这些其他因素被包含在误差项U中。为了简洁，我们不失一般性地假设，E和U在总体中相互独立（没有共同前因，一方不导致另一方）。这样总体中E与I之间的边缘关联就可以识别因果效应E→I。然而，有向无环图告诉我们，I是个在处理与误差项间的碰撞变量，E→I←U。将样本限制在低收入者中，等于对这个碰撞变量做条件化。结果就是，现在E与I之间的关联有两种来源：表示我们感兴趣的因果效应的因果路径E→I，以及新引入的非因果路径E---U→I。样本截取导致了内生选择偏倚，使得在被截取样本中E与I之间的关联不能识别E对I的因果效应。

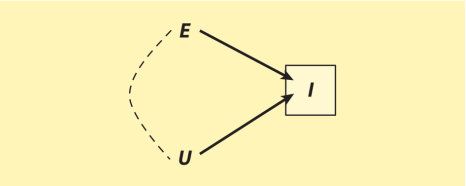
图5

这个例子说明了个重要的一般要点：如果一种处理T，对结果Y有效应，T→Y，那么结果就是处理T与结果的误差项U的路径上的碰撞变量，T→Y←U。因此，直接对结果进行选择，或是对受结果影响的变量进行选择，总会有潜在问题。

无应答偏倚（nonresponse bias）。导致截取偏倚的因果结构同样在回溯性研究中的无应答偏倚中存在。仅有的区别是，与其将无应答理解成对结果本身的条件化，理解成对受结果影响的变量的条件化更好。让我们考虑Lin et al. （1999）所讨论例子的简化版。例子中要估计离婚父亲的收入对他们儿女金钱支持的影响。我们讨论的是无应答会怎样影响这样一种估计（图6）。一个已离婚父亲的收入I，以及他对子女所支付的金额P，都影响这个父亲会否回复研究的应答R（在不失一般性的前提下，我们忽略I与P可能会有共同前因）。应答行为因此是处理与结果间非因果路径上的一个碰撞变量，I→R←P。只分析完成的访谈，丢弃没有回应的父亲（成列删除），就等同对这个碰撞变量做条件化，会引入父亲收入与子女支持支付额之间的非因果关联（就是内生因果偏倚）。

图6

确认偏倚（ascertainment bias）。研究精英成就的社会学研究有时候会使用非随机样本。这是因为全体人群中搜集数据的成本太过昂贵，或者是因为随机抽样不太可行。这样的研究可能会选择对所有已经有了精英地位的个人、组织或是文化产品进行取样（比如说，是最高法院的大法官，进入了财富500强排行榜，或是受到了重要的赞赏），然后对有别的特征的个人、组织、文化产品进行抽样（如，在联邦法院做法官，申报收入超过1亿，或是商业上成功），让他们成为控制组。这种方法的逻辑是，通过比较最成功的跟稍微不那么成功的案例，就可以发现什么让他们脱颖而出。问题在于，通过只有成功者的样本来研究成功的原因，就是引狼入室，会引入内生选择偏倚。

我们怀疑，这种抽样策略可能可以说明最近那个震惊四座的对音乐行业中成功决定因素的研究的结论（Schmutz 2005; 又见 Allen & Lincoln 2004, Schmutz & Faupel 2010）。那个研究设定的目标是识别音乐专辑的商业成功对被收录到滚石杂志大肆吹嘘的500 Greatest Albums of All Time的几率的影响。该样本包括了大概1700张专辑：所有被收录的500张专辑，以及额外的1200张专辑。所有专辑都赢取了某种精英特性，比如在Billboard排行榜中排在榜首，或是赢了批评家中的民意调查。美国几十年间发行了数以万计的专辑。他们明显是这之中的一部分，很大程度上因成功而被选择出来。在分析前，大家可能预料的是在商业取得杰出成就（如排在Billboard榜首）会增加专辑进入滚石500的概率（因为编排列表的专家只会考虑他们知道的专辑。他们可能知道所有曾排在榜首的专辑，却不可能知道所有发布过的专辑）。令人惊讶的是，对样本的Logistic回归表明排在Billboard榜首跟被滚石500收录有强烈的负关联。

为什么会这样？就像作者所说的，我们应该谨慎看待这个结果（Schmutz 2005, p. 1520; Schmutz & Faupel 2010, p. 705）。我们猜想内生选择偏倚是这个结果的元凶。图7中的有向无环图说明了我们的论点（为了清晰起见，我们不在研究中考虑额外的解释变量）。结果R是专辑被收录到滚石500中。处理B是在Billboard中排榜首。我们预估它在全体专辑的范围内会对R有正面效应。这样设计，R和B都对被收入到样本中S有很强的正效应。分析这个样本就意味分析时对被样本包含S做了条件化，而S是在处理与结果的非因果路径中的碰撞变量，B→S←R。对这个碰撞变量条件化改变他的直接前因R与S间的关联性，且引入了内生选择偏倚。若样本挑选得足够严格，那么偏倚就会大到能够扭转B对R估计效应的符号，生产出实际上为正的效应的负面估计。

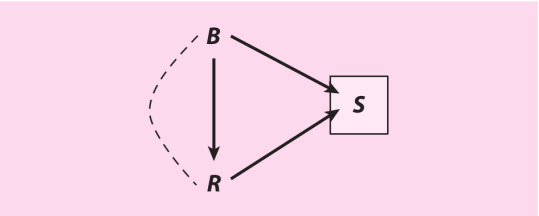
图7

表1的意思是一样的。对于二元变量B和R，B=1表示在Billboard排榜首，R=1表示被收录进滚石500，0意义则相反。单元格中的计数a，b，c，d表示出了总体中所有专辑。在没有共同前因引起的混杂效应（图7中那样）时，总体中比值比OR=ad/bc给出了B对R的真实因果效应。现在留意，大多数专辑从未进过榜首，也未被收录进滚石500。为了减少数据搜集带来的负担，研究只将所有R=1和所有B=1的专辑纳入到分析，对不那么成功的专辑严重缺乏采样，a_s < a。在这个样本中，R对B效应的Logistic回归中的比值比与真正的比值比相比，就会有向下偏误，甚至可能方向相反，OR_s = a_s * d / bc < ad / bc = OR_p。

表1

我们留意到，即使结果被直接选择了，如果对数据加上某些约束，我们有时候还是能够还原出因果信息。流行病学中病例对照研究（case-control studies）的领域（Rothman et al. 2008）和计量经济学中研究基于应答或基于选择的抽样（response- or choice-based sampling）的文献（Manski 2003, ch. 6）处理的问题。然而，在病例对照研究中，有条关键准则就是所抽样的观察不应同时受处理和结果影响。违背了这一准则的结果就是确认偏倚（Rothman et al. 2008）。本例子中内生选择偏倚就是确认偏倚，因为控制组的专辑抽样时同时（a）没有收录进滚石500，和（b）有商业成功。（Greenland et al. 1999和Hernán et al. 2004运用有向无环图，将不少有趣的生物医学病例对照研究中的确认偏倚看作是内生选择偏倚来研究）

Heckman选择偏倚（Heckman selection bias）。Heckman选择偏倚可能是社会科学中最广为人知的选择偏倚了。它可以被阐述成内生选择偏倚。有个经典例子讲的是做妈妈（就是有了孩子）M对潜在雇主给这位女性出的工资W_O的影响（Gronau 1974, Heckman 1974）。图8画出了相关的有向无环图。按照标准劳动力市场理论，我们假设做妈妈会影响一位女性的保留工资W_R，也就是让她走出家、成为劳动力的必要工资。就业E同时受邀约工资和保留工资的影响，因为她只会在邀约工资达到或者超过她的保留工资时才会接受工作。因此，就业就是路径M→W_R→E←W_O上是否是妈妈与邀约工资间的碰撞变量。（为了简洁起见，假设M和W_O没有共同前因。）

图8

很多社科数据集包含是否为母亲M的信息，但他们通常不包含女性的保留工资W_R的相关信息。重要的是，数据中通常只有在职女性才有邀约工资W_O的信息。如果分析者将分析限定到在职女性的范围内，他就会对碰撞变量E进行条件化，打开了从做妈妈到邀约工资的非因果路径，M→W_R→[E]←W_O，引入内生选择偏倚。这个分析会因此引入做妈妈与工资间的关联，即使做妈妈对工资的因果效应实际上为0（图8a）。

即使是做妈妈对邀约工资没有影响，图8a那样，内生选择的问题也已经够糟糕了。使得问题更加复杂的是，做妈妈可能确实对邀约工资有影响（如因为做妈妈的女性的生产力不同或是遭到歧视的缘故）的可能性。图8b中添加的箭头M→W_O表示了这个可能性。这个小小的修改产生了第二个内生选择问题。就像上面说的那样，如果处理对结果有影响，结果都会是处理与误差项路径上的碰撞变量。对E条件化现在更等同于对在路径M→[W_O]←ε上碰撞变量W_O的派生变量条件化。这引入了做妈妈与误差项间的非因果关联性，M---ε→W_O。注意，第二个内生选择偏倚即使在非碰撞变量W_R被测量及控制后仍会存在（但第一个不会）。

对这两个内生选择问题的区别的了解，让我们有机会尝试文献中还没人用的非参数识别方法：分析者可以通过控制女性的保留工资，非参数地测试做妈妈对邀约工资没有效应的因果性零假设。如果在对W_R和E条件化后，M和W_O没有关联，那么M对W_O没有因果效应，就像图8a那样。对因果效应M→W_O的大小的非参数识别，却是本质上不可能的，如图8b。即使W_R被观察到了、被控制了（因此阻断了非因果路径M→[W_R]→[E]←W_O上关联性的流动），条件化E仍会创造出非因果路径 M---ε→W_O。因此，对W_R和E条件化后，M与W_O间的关联性的大小有偏误，不能用以估计因果效应的真实大小。

增加额外的假设，我们还可以预测偏误的方向。具体来说，可以假设图8中的因果效应对于所有女性来说方向相同（VanderWeele & Robins 2009b）。比方说，如果做妈妈通过增加保留工资减少就业的可能，同时对于所有女性来说，更高的邀约工资会增加就业的可能，那么在职妈妈的平均工资必定比在职的没有孩子的女性高。因此，样本限定在在职女性的经验分析会低估做妈妈的工资惩罚。这正是Gangl & Ziefle （2009）对做妈妈的工资惩罚的矫正选择性分析后得出的结论。

5.2条件化中间变量

方法论学者警告了很久：条件化受处理影响的中间变量会导致偏倚（如Heckman 1976; Berk 1983; Rosenbaum 1984; Holland 1988; Robins 1989, 2001, 2003; Smith 1990; Angrist & Krueger 1999; Wooldridge 2005; Sobel 2008）。这种偏倚以很多种面目出现。它是纵向研究中基于已知信息的截取、损耗偏倚的来源，是社科的机制研究中中介分析、直接间接效应估计的中心。跟从Pearl （1998）、Robins （2001）、Cole & Hernán （2002）的做法，我们将中间变量条件化的问题处理成内生选择偏倚，用有向无环图来说明问题。

纵向研究中的基于已知信息的截取（依从性截取；informative/dependent censoring）和损耗偏倚（attrition bias）。绝大多数前瞻性的纵向（面板）研究整个研究时段内都会遇到失访的问题。在基线处进入研究的参与者可能去世了、搬家了，或就是仅仅不愿继续回答问题。随着研究的继续，可用于分析的个例数减少，有时候是大规模地减少（如Behr et al. 2005, Alderman et al. 2001）。当不能跟踪所有人时，有些社会学研究就只分析可以分析的个例。事件史分析和生存分析取向会分析各个个例，直到他们脱落（截取），而其他的分析手段则可能完全丢弃没被完整跟踪的个例。这两种实践都可能导致内生选择偏倚。

我们的例子改编自Hill（1997）对损耗偏倚的分析。考虑在一个有损耗C的前瞻性研究中估计贫穷P对离婚D的效应。图9画出了导致损耗的各种情形。图9a显示的是最温和的情形。这里，P影响D，但两个变量跟C都没有因果关系——损耗相对于处理与结果而言是完全随机的。如果这个假设是正确的，那么只分析完整的个例（也就是对没有损耗条件化）也完全不会产生问题；因果效应P→D无需任何对损耗的调整就可被识别。在图9b中，贫穷被假设会影响脱落风险的大小，P→C。尽管如此，我们仍然可以直接识别P→D的因果效应。同图9a类似，对图9b中的C条件化不会导致偏倚，因为条件化C不会打开任何P与D之间的非因果路径。然而，如果有未测量因素U（例如婚姻问题）同时影响损耗和离婚，就像是图9c那样，那么C就成了贫穷与离婚非因果路径上的碰撞变量，P→C←U→D。对C条件化会打开这条路径，扭曲贫穷与离婚之间的关联。因此，损耗偏倚就不过是内生选择偏倚罢了。注意，即使损耗本身很大，也不一定成为因果识别的问题。如果对损耗做条件化打开了处理与结果间非因果路径，像图9c那样，损耗就会产生问题（更多更详尽的损耗情形，见Hernán et al. 2004）。

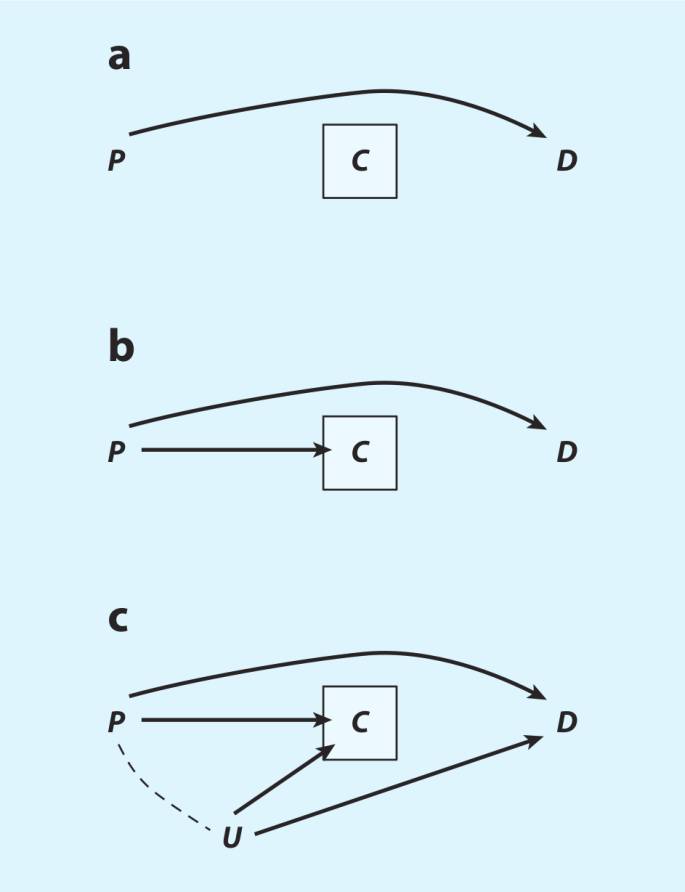
图9

被处理影响的不完美代理测度（proxy measure）。很多社会科学研究研究受学校教育对各种产出——如认知（如Coleman et al. 1982）、婚姻（如Gullickson 2006, Raymo & Iwasawa 2005）、工资（如Griliches & Mason 1972, Leigh & Ryan 2008, Amin 2011）——的影响。学生接受的学校教育当然不是随机的：平均来说，先天能力更高的个体更有可能获得更多的学校教育，也更可能在人生的后来阶段获得良好的结果。在没有对先天能力的令人信服的测度的情况下，研究者常转而使用先天能力的代理测度，像是IQ类的认知测验的分数。使用有向无环图，我们会说明三种不同问题的区别，以此详细解释计量经济学中对代理-控制策略的讨论（如Angrist & Krueger 1999; Wooldridge 2002, pp. 63-70）。

具体地讨论。考虑受学校教育S对工资W的效应。图10a表示了先天能力U，通过打开非因果路径S←U→W，混杂了受学校教育对工资的效应，这么种常见假设。因为真正的先天能力没有被观察到，不能关闭路径，效应S→Y也就没有被识别。接着，分析者可能将测量到的测验分数Q作为对没有观察到的U的代理，对它做控制，就像图10b那样。就U对Q有强烈影响的部分而言，Q是对U的有效代理。但就Q不能完美地测量U的部分而言，S对W的效应还是部分地被混杂了。这是代理控制的第一个问题——当指标（如测验分数）不能完美地捕获想要的潜在建构（即能力）时有残差混杂的熟悉问题。不管如何，在图10b的假设情况下，对Q做控制至少会去除部分U带来的混杂偏倚，而不会引入新的偏倚。

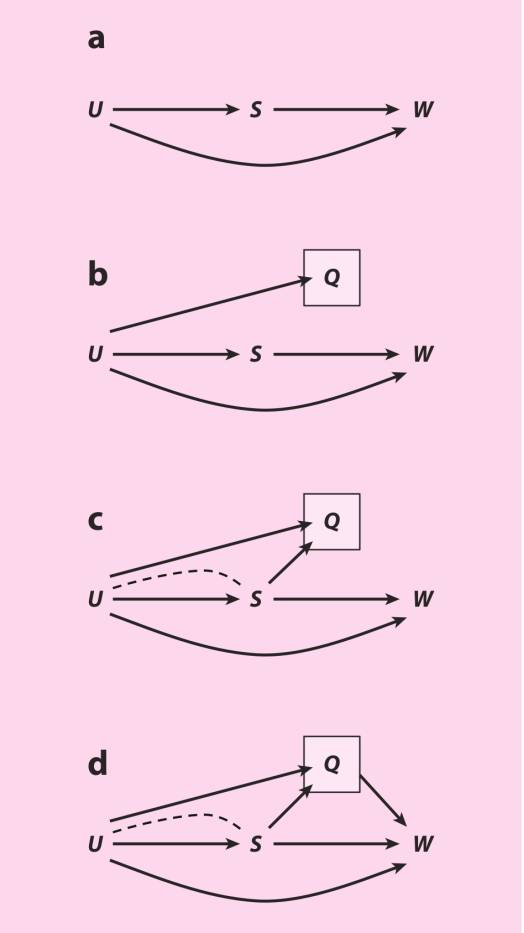
图10

第二个问题，内生选择偏倚，在图10c中进入视线。认知测验分数有时候是在受测者接受了学校教育后才被测量出来的。这是个问题，因为我们已知学校教育会影响学生的测验分数（Winship & Korenman 1997），同新增的箭头S→Q显示的那样。这让Q变成了受学校教育到工资的非因果路径上的碰撞变量，S→Q←U→W。对Q条件化会打开这条非因果路径，引致内生选择偏倚。

第三个独特的问题来源于Q自身可能会对W有直接的因果效应，Q→W。可能是因为雇主会在招聘过程中使用测验分数，不管应聘者的受教育情况如何，对高分者给予奖励。如果是这种情况，受学校教育对工资的因果效应会被测验分数在因果路径S→Q→W上部分中介。对Q做控制会阻断这条因果路径，导致过度控制偏倚。

三重夹击让分析者进退两难。如果Q是在接受学校教育后才测量的，分析者是应该控制掉Q，来（通过代理）去除部分U带来的混杂？还是应该不要控制Q，以防引入内生选择偏倚、过度控制偏倚？没有对有向无环图中各种效应的相对强度的仔细了解（这些知识很难获得，尤其是有未观察变量时），我们难以确定哪个问题应主宰经验研究中的考虑，也难以判断应采取何种行动。

直接效应，间接效应，因果机制，以及中介分析（mediation analysis）。用于估计直接效应与间接效应的常见方法（Baron & Kenny 1986）极容易遭受内生选择偏倚。我们首先看直接效应的估计。为了明确概念，考虑STAR项目那种对班级大小的实验应该怎么分析。分析问题是，一年级的班级大小T，是否会通过某种除提高三年级时学生的成就M外的机制，对能否从高中毕业Y产生直接效应（Finn et al. 2005）。因为班级大小被随机化了，T和Y没有共同的前因，而处理T对结果Y的总效应可以被他们的边缘关联识别。但处理后的中介变量M，却没有被随机化，因而可能跟结果Y有着共同的未测量前因U。U可能是父母的教育程度、学生的动机水平，以及其他任何没有在研究中被明确控制的M和Y的混杂变量。U这样的存在会使得M成为处理与结果间非因果路径T→[M]←U→Y上的碰撞变量。为了估计T→Y的直接因果效应而对M做条件化（比如以T、M为解释变量回归Y），会打开这条非因果路径，引入内生选择偏倚。因而，T对Y的直接效应没有被识别。

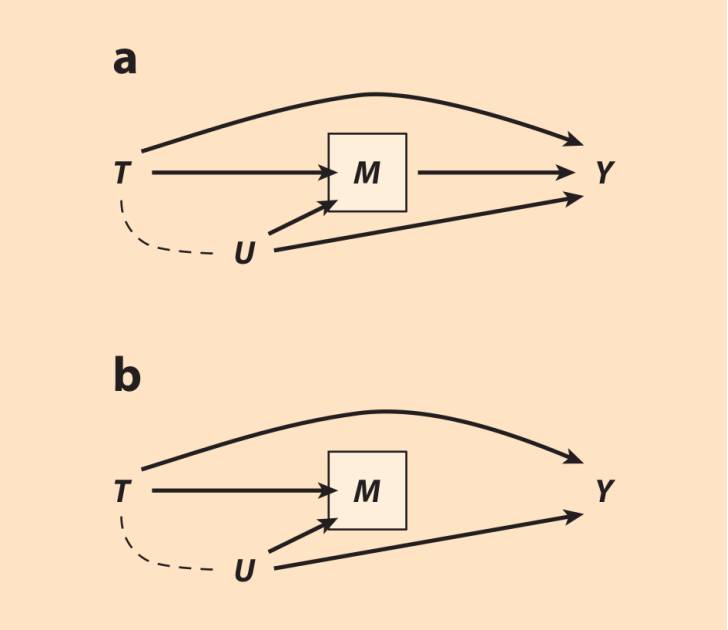
图11

通过比较T对Y的总效应估计和直接效应估计的差异，来尝试检测间接效应的做法（Baron & Kenny 1986），也会遭受类似的内生选择偏倚。为了论述方便，我们假设，在三年级的成就对高中毕业与否没有因果效应（图11b）。T对Y的总效应因此等同于T对Y的直接效应，因为T对Y没有由M中介的效应。给定M，T与Y之间的条件关联却跟T对Y的总效应有区别，因为M是个碰撞变量，条件化碰撞变量通过T→[M]←U→Y引入了T和Y之间的非因果关联。因而，对总因果效应的正确估计跟T对Y直接效应的（朴素而有偏误的）估计不同。分析者可能会做出错误结论，即使在间接效应不存在时，也认为它存在。

对于当前社会学的经验研究来说，中介分析中的内生选择问题特别重要。传统上探讨控制未观察混杂效应的文献集中讨论的是主处理的混杂变量，却没有关注中介变量的混杂变量。因果中介分析的现代文献中会讨论被估计变量还有非参数识别的条件（Robins & Greenland 1992; Pearl 2001, 2012; Sobel 2008; Shpitser & VanderWeele 2011），也会讨论参数和非参数的估计策略（VanderWeele 2009a, 2011a; Imai et al. 2010; Pearl 2012）。

5.3条件化在处理变量前的碰撞变量

对在处理前的变量做控制有时候会增加偏误，而非减少偏误。分析者应该小心一类在处理前的变量——处理前的碰撞变量（Pearl 1995, Greenland et al. 1999b, Hernán et al. 2002, Greenland 2003, Hernán et al. 2004, Elwert 2013）。

社交网络分析中的同质相吸偏倚（homophily bias）。社交网络分析中的因果推断有个经典问题：相互之间有社会连结的个体之所以会呈现相似的行为，不是因为一个个体会影响其他个体（因果），而是因为相似的个体更可能在彼此间建立联系（同质相吸）（Farr 1858）。将同质相吸与人际因果效应（也叫同侪效应、社会传染、网络影响、感应、扩散）在同质相吸的来源未被观察到（是潜在的）时特别困难。Shalizi & Thomas （2011）最近解明，潜在同质相吸偏倚是一种先前我们所不知的内生选择偏倚。在这里，社会连结本身起到了处理前碰撞变量的作用。

例如，考虑市民参与在朋友间的扩散。以（i, j）的二元关系索引朋友关系（图12）。问题是，个体i在时间t的市民参与Y_i(t)会否导致后来个体j的市民参与Y_j(t+1)。为了解说得更明白，假设市民参与不会在朋友间扩散（也就是没有Y_i(t)→Y_j(t+1)的箭头）。作为替代，假设每个个体的市民参与都是由他们本身的特性U（比如说利他主义）导致的。特性U至少有一部分没有被观察到（给定箭头Y_i(t)←U_i→Y_i(t+1)和Y_j(t)←U_j→Y_j(t+1)）。同质相吸是形成连结的原因，以使利他的人群之间会形成优先连接（preferential attachments），U_i→F_i,j ←U_j。因此，F_i,j是个碰撞变量。因此，计算朋友间的关联性就意味着分析时条件化社会连结的存在，F_i,j=1。这个就是问题所在。对F_i,j条件化打开了处理与结果间的非因果路径，Y_i(t)←U_i→[F_i,j]←U_j→Y_j(t+1)，导致i的市民参与与j的市民参与产生关联，即使一者没有导致另一者。

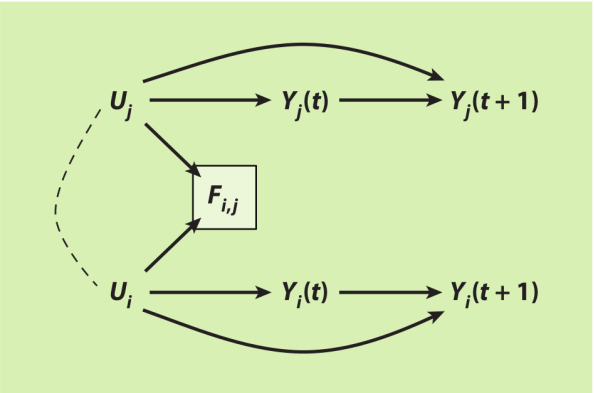
图12

总结，如果连结的形成或是解除受未观测到的变量影响，而这些未观测变量分别与一个个体的处理变量和另一个个体的结果变量有关联，那么寻找人际效应就会在网络的个体间引入伪关联（就是内生选择偏倚）。

这个问题的一个解决办法是将形成和解除显式建模（Shalizi & Thomas 2011）。在图12的模型中，测量并条件化个体i的促使连结形成的特性U_i，又或者是个体j的U_j，或者同时测量两者，都可以达到显式建模的效果。使用其他办法解决潜在同质相吸问题的文献正不断增多。比如，Elwert & Christakis （2008）引入了种测量及减少同质相吸偏倚的代理策略；Ver Steeg & Galstyan （2011）提出了种对潜在同质相吸的正式检验；VandeWeele （2011b） 介绍了种正式的敏感性分析；O’Malley et al. （2014）探索了如何用工具变量来达到目标；VanderWeele & An （2013）对这些文献做了大量考察。

哪些处理前变量应该被控制？在社交网络分析之外，处理前碰撞变量也有实际意义和概念性意义。有的经验研究对处理前变量进行控制的结果是偏误明显增加，而非减少。打比方说，Steiner et al. （2010）报告了个研究内比较。该研究比较不同方法对某种教育干预对学生测验分数的影响的估计。他们将实验得出的估计作为基准，与观察性研究得出的估计做比较。在观察性研究中，仅控制在处理前的心理倾向或是仅控制在处理前的词汇量测验分数，会使处理对数学分数的估计效应的偏误增加大概30%。不仅如此，他们发现，尽管对额外的处理前变量进行控制一般会减少偏误，但有时候额外的控制也会增加偏误。这些偏误的增加有可能是因为控制了处理前碰撞变量。

这使得观察性研究中的控制变量选择更令人疑虑了。分析者应该控制哪些处理前变量？哪些处理前变量最好撒手不管？看了图13中的有向无环图后就明白，不追究数据具体是如何生成出来，我们不可能回答好这些问题。先比较图13a与13b中的有向无环图。两个模型中，处理前变量X都跟常识中对混杂纯粹关联性的定义吻合：（a）X时间上先于处理T；（b）X与处理相关联；（c）X与结果Y相关联。传统建议就会是在两种情形下都对X条件化。

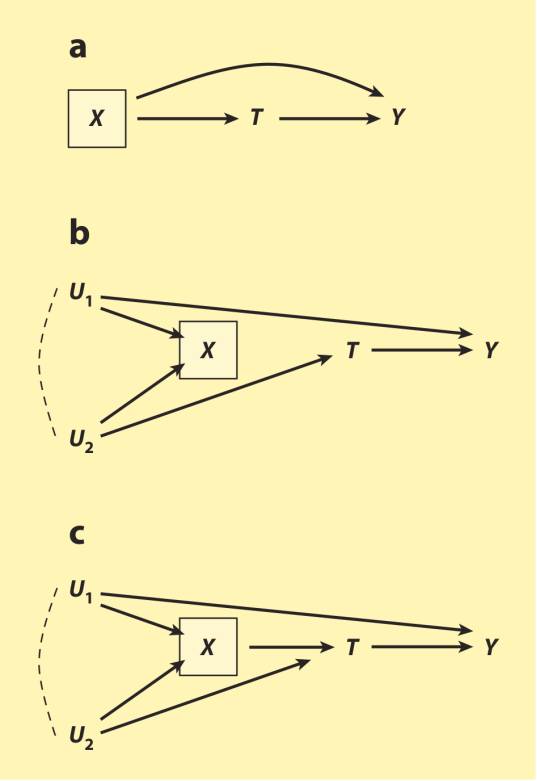
图13

但这个传统建议不正确。怎样做才对，跟数据是怎样生成的息息相关（Greenland & Robins 1986, Weinberg 1993, Cole & Hernán 2002; Hernán et al. 2002, Pearl 2009）。在图13a中，X确实是个共同前因、混杂变量，因为它就在处理与结果间开放的非因果路径上，T←X→Y。条件化X会阻断这个非因果路径，使T对Y的因果效应得到识别。相比起来，图13b中，X是阻断处理与结果间的非因果路径T←U_2→X←U_1→Y的碰撞变量。条件化X会打开这条非因果路径，引入内生选择偏倚。因此，如果数据是图13a那样生成的，分析者应该条件化X；但如果数据是图13b那样生成的，她就不该条件化X。

如果U_1和U_2没有被观察到，分析者无法通过经验研究区分出图13a和图13b，因为两者对观察的内在意义都一样。两个模型中，X、T、Y的所有组合都相互之间有边缘关联和条件关联。因此，唯一能够决定要不要控制X的方法，就是从先验的立场上来决定哪个模型准确地表示出了数据生成过程。换句话说，怎样选择控制变量，需要在理论上对数据生成模型有所阐述。

在实践中，社会学家可能没有一个完全缜密的数据生成理论。但其实不完整的理论就足以决定该选择哪些处理前控制变量了。如果分析者愿意假定控制可观察的处理前变量的某种组合就足以识别处理的总因果效应的话，那么将所有处理或是结果或两者的前因（直接或间接地）控制掉，就足够了（VanderWeele & Shpitser 2011）。

这个建议的好处在于它防止了分析者对在处理前的碰撞变量做控制。在图13a中，它准确地建议我们控制X（因为X是处理和结果的共同前因）。而在图13b中，它准确地建议我们不要控制X（因为X既不导致处理也不导致结果）。

尽管如此，这个建议仍依赖于数据生成的某种理论，不管这种理论多么粗糙，还是要有某种充分的已观察控制变量集。留意在图13c中这样的变量集就不存在。在此，X既是个在非因果路径T←X←U_1→Y和T←X←U_2→Y上的混杂变量，又是在非因果路径T←U_2→X←U_1→Y上的碰撞变量。控制X会去除混杂效应，但却会引入内生选择，不控制X则相反。简要来说，没有一个处理前控制变量集能够识别T对Y的因果效应，因此VanderWeele & Shpitser （2011）的规则不适用。Greenland （2003）建议，当有向无环图中所有变量都是二元的时候，控制一个既是混杂变量，又是碰撞变量的变量（如图13c那样），减少的偏误很可能（但不一定）比增加的偏误多。

6. 讨论与总结

在本综述中，我们提出，理解内生选择偏倚是理解在社会学中如何识别因果效应的关键。援引近来在计算机科学理论（Pearl 1995, 2009）和流行病学（Hernán et al. 2004）的工作，我们将内生选择阐述成有向无环图中对碰撞变量条件化的问题。我们先审查了从非因果的关联中分离因果性的必要步骤，接着看到了内生选择逻辑上跟混杂偏倚和过度控制偏倚同样重要，因为所有的非参数识别问题都可以被还原成混杂（没有条件化共同前因）、过度控制（条件化了因果路径上的变量）和内生选择（条件化了碰撞变量），或是三者的混合（Verma & Pearl 1988）。

方法论上的警告容易理解时，警告最有效（Pearl 2009, p. 352）。我们相信有向无环图为我们提供了这样一种语言，因为他们让分析者的注意力集中在对因果效应的非参数识别最重要的东西上：变量间因果关系的质性假设。这并不是说代数或是参数假设在社科方法论中没有意义。但只要代数表示阻碍了应用研究者对方法论问题的了解，以图的方式来表述方法论问题可能会提高研究者在实践中对这些问题的意识。

在本文的主要部分中，我们说明了因果推断中的很多问题可以被阐述成内生选择偏倚。有个洞见就是，对内生变量（碰撞变量）做控制，无论它在时间上与处理和结果的相对位置是什么，都会引发新的、非因果的关联，很可能会引致有偏误的估计。我们根据碰撞变量与处理和结果在时间上的相对位置区分了三种内生选择问题。对前两种情况——结果后的和在之间的碰撞变量——可以直接给出一般性的建议：当估计总因果效应时，避免条件化处理后变量（Rosenbaum 1984）。当然，在实践中研究者可能很难跟从这个建议，因为条件化会藏在数据收集计划中，或是藏在选择性无应答、损耗的结果中。即使有些地方跟从这个建议比较容易，当公开声明的兴趣跟因果机制、中介、直接或间接效应这些需要凝视处理后黑箱的议题相关时，它也很难下咽。不过，结合了概念上的仔细、潜藏假设的意识、强力的敏感性分析的新的因果机制估计方案很快就可用了（Robins & Greenland 1992; Pearl 2001; Frangakis & Rubin 2002; Sobel 2008; VanderWeele 2008a, 2009b, 2010; Imai et al. 2010; Shpitser & VanderWeele 2011）。

怎样对待处理前的碰撞变量的建议就比较难给出了。如果知道了处理前碰撞变量没有同时是混杂变量，那么解决办法就是当可能时不要对它条件化（在社交网络分析中这是不可能的，因为在处理前的社会连结隐含在研究问题里）。如果处理前碰撞变量同时是个混杂变量，条件化它，通常去除的偏误比引入的偏误多（Greenland 2003），特别是分析还对其他很多处理前变量条件化了的时候（Steiner et al. 2010）。某些情形里研究者可以用工具变量估计，虽然研究者应该要了解它的局限性（Angrist et al. 1996）。

如果不能完全避免内生选择偏倚，处理内生选择的遗留困难之一是我们很难预测偏误的符号及大小。没有强的参数假设，偏误的大小和符号依赖于有向无环图的具体结构、具体效应的大小、效应在个体间的变异以及变量的分布（Greenland 2003）。传统上对偏误大小与符号的直觉判断在线性模型的假设失效时可能会以难以预料的方式失效。尽管如何，近年来统计学学者推导出了重要（同时经常是复杂的）的结果，在应用研究中已经被证明很有威力。举例说，VanderWeele & Robins （2007a, 2009a,b）推导出了在二元变量、单调效应、没有交互作用的有向无环图中内生选择偏倚的符号。Hudson et al. （2008）在疾病家族分类研究中有意义地使用了这些结果。

尤其是，Greenland （2003）推导出了在二元变量有向无环图中内生选择偏倚和混杂偏倚的相对大小的近似，是很有用的结果（也见 Kaufman et al. 2009）。他的三条经验准则跟我们的分类十分相合。首先，对结果后碰撞变量条件化，T→[C]←Y，产生的偏误会跟对应的混杂偏倚T←C→Y一样。其次，对中间碰撞变量条件化可能会产生比指向碰撞变量的效应更大的偏误，尽管在中间碰撞变量本身对结果没有效应时，偏误会比这些效应小。最后，对处理前碰撞变量条件化（如图12和13那样）通常引起的偏误小。这也正是为什么将潜在同质相吸偏倚看成是内生选择（而非混杂偏倚）是对社交网络分析的人来说是个好消息。进一步，如果处理前变量既是碰撞变量又是混杂变量（如图13c），那么条件化它可能去除的偏误比引发的偏误多，尽管还是没有做到非参数识别。可是，我们要警告，这些对二元变量有向无环图适用的经验准则不一定能够推广到变量有着不同分布的有向无环图中。我们需要更多研究，来理解现实社会科学场景中内生选择偏倚的方向和大小。

社会学中的经验研究目标很多样，包括描述、理解，还有因果推断。既然无假设的因果推断并不可行，社会学者必须依赖理论、严谨实质的观察，以及牢靠的先验知识来评估偏倚的威胁。使用有向无环图，社会学者能够形式化地分析他们理论假设的后果，决定因果推断是否可行。当分析有保证时，这样的分析会让人们对因果性判断更有信心；当因果性判断不恰当时，这样的分析能够明确说明可能存在的偏倚——包括内生选择偏倚在内。